A regular video signal has a voltage range from 0mV to 700mV. Digitally coded it is represented as code zero for black code 255 for white. Theoretically this could be a linear function between the two 'end points' black and white. But human vision has a nonuniform perceptual response to luminance and display devices also are nonlinear. To create a satisfactory image the range from black to white cannot be coded linearly, it must be coded in accordance to the nonlinear properties of the human perception and the nonlinear properties of the display device. In any display device a frame buffer value of e.g. 50 will never give half the brightness of a value of 100.
Changing gamma only all grey areas are changed and the 'end points' as total black and total white remain unchanged. Practically these unchanged 'end points' are achieved by a normalization algorithm within the gamma correction circuit.
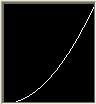
All display devices are nonlinear. This means if supplied signal voltage is doubled the achieved brightness does not double. It varies approximately as the square of the voltage, having a gamma of "2".
The term gamma was coined by the electronics industry describing the intensity I (brightness) of a cathode-ray tube (CRT) for a given voltage. Gamma is the exponent to the voltage determining the relationship between voltage and brightness.
With a higher value for gamma (higher than "1") a higher contrast is achieved in the higher range (grey to white) and a lower contrast is achieved in the lower range (grey to black). The image seams darker because the brighter area is more graduated and the darker area is less graduated.
With a lower value for gamma (lower than "1") a lower contrast is achieved in the higher range (grey to white) and a higher contrast is achieved in the lower range (grey to black). The image seams brighter because the brighter area is less graduated and the darker area is more graduated.
Note that with conventional film, 'gamma' is more a synonym for contrast: higher gamma means higher contrast and lower gamma means lower contrast by changing the 'photographic density'.
Creating a video signal fitting to the human perception the luminance of each of the three basic signal layers red, green and blue must be transformed to establish a "nonlinear" video signal. The perceived brightness increases in the darker region faster than in the brighter region. The human eye has a gamma of about 0.3 to 0.5.
The entire signal chain from a camera to the electronic display devices built to reproduce an original image must have a gamma correction to create the same visual sensation as the original natural image.
CRT monitors and all modern displays usually should be built with a gamma value of about 2.2, but units vary between about 1.4 and 2.5. With a gamma of 0.45 to 0.5 the display gamma of 2.2 would be compensated to a value of "1".
Gamma correction generally consists of applying the inverse of the display transfer function to the image before the display device.
| high gamma of display device (e.g. 2.2) |
| gamma correction (e.g. 0.45) |
| resulting image with linear appearance |
The compensation of the nonlinearity of the display devices is done by adding a transfer function to the display card. But different manufacturers chose different default compensations, resulting in different colors on different computer setups providing the same numeric color values. The color with the same numeric RGB values looks brighter on a Mac or SGI when it does on a PC. PC displays usually have a gamma of 2.2 and MAC displays have a gamma of 1.8. An image composed in e.g. Photoshop on a Mac will look too bright on a PC displays and vice versa! In general it is advisable to create content with the linear gamma of "1" and make the necessary adjustment at the display device in or right before the display device (in the signal chain) but to not distort the image depending of the used computer or display system.
 |
 |
 |
 |
 |
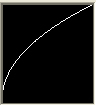 |
| gamma correction = 0.5 | gamma correction = 1 | gamma correction = 2.2 |
Gamma is measured by measuring the light intensity on a linear scale.
The basic procedure is to set up the monitor as it will be used (brightness, contrast, etc.) and to display an area of a specified digital value. By varying the digital value, we can fit the resulting transfer function in log-log space, and come up with a value for gamma.